Dynamic Tensor Rematerialization(DTR)
Marisa Kirisame, Steven Lyubomirsky, Altan Haan, Jennifer Brennan, Mike He, Jared Roesch, Tianqi Chen, Zachary Tatlock
- Save memory for NN by dynamically discarding and recomputing intermediate results at runtime.
- By being smart about what to keep and what to discard, train larger models under a tight budget.
- Save 3x memory for 20% extra compute time - train models 3x as large!
- DTR Makes no assumptions about the model, and does not require a static graph.
- DTR can be easily implemented into different deep learning frameworks.
- DTR still achieves amazing space-time tradeoff!
Adoption:
MegEngine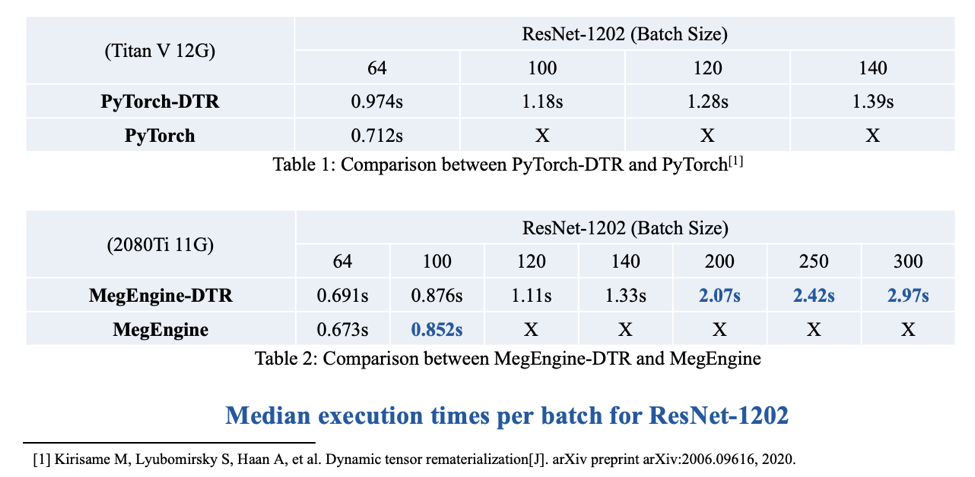
Raf
| Model | Maximum non-remat batch size | Remat batch size | Throughput relative to non-remat |
|---|---|---|---|
| BERT-base-mlm | 16 | 32 | 94.3% |
| BERT-large-mlm | 8 | 16 | 96.5% |
| GPT2 | 8 | 24 | 93.2% |
Inspired:
DELTATechnical Dive
- Gradient Checkpointing is a technique to save memory for Deep Neural Network training.
- Or more generally, for reverse-mode automatic differentiation.
- However, memory planning is np-complete.
- Checkpointing also has to deal with program with arbitary control flow.
- To combat this, previous work made different restriction which sacrifice performance or usability.
- Some works models the program as a stack machine with no heap...
- And suffers performance degradation when the assumption is broken!
- (For example, NN with highway connection/branching).
- Other works use an ILP solver, which consume lots of time to find the optimal memory planning.
- And can only be used for program/framework without control flow, posing problem for real world adoption.
- Additionally, gradient checkpointing couple derivative calculation, with memory saving by recomputing.
- This add complexity and limit applications range.
- DTR tackles the problems above by planning the memory greedily at runtime, instead of as a compiler pass.
- Essentially, DTR always pair each tensor with a thunk(think lazy evaluation), so all tensors can be recomputed after evicting.
- This solves the control flow and stack machine issue, as we do not model the program in anyway!
- However, with a novel cache eviction policy, we are still able to achieve great performance.
- Suprisingly DTR 'accidentally' discovered the O(n) time O(n^0.5) space, and the O(n log n) time O(log n) space scheme.
- These two are both well-known result.
- Furthermore DTR switch smoothly between normal execution without recomputation, O(n^0.5) space scheme, and O(log n) space scheme .